ENGINEERING MECHANICS , TYPES OF BEAM ,TYPES OF LOADING, TYPES OF SUPPORT

ENGINEERING  MECHANICS PART 1  , TYPES OF BEAM ,TYPES OF LOADING, TYPES OF SUPPORT

engineering mechanics is divided into two parts 

1)static: 

                       (in statics object's  at rest like we apply force on the wall )

2) dynamic:

                         (in dynamic objects are under the action of forces like force tends to give motion to the object or stop the motion of the object)

dynamic is further divided into two parts :

(a) kinematic (time-space relationships)

(b) kinetics

1  System of forces :

a: collinear forces (line of action of forces are same)

in this  diagram f1 and f2 are colinear forces

b: concurrent forces(forces acting on the same point

c: co-planar forces(forces acting on the same plane )

here all the forces in xy plane 

d: co-planar concurrent forces

here p1,p2,p3 and p4 are in same plane xy and passing through the same point O

e: co-planar non-concurrent forces

f: non-coplanar concurrent forces

g: non-co-planar nonconcurrent forces

h: like parallel forces

i: unlike parallel forces

2 Composition and resolution of force :

(a) parallelogram law of forces: 

Let P and Q be two vectors acting simultaneously at a point and represented both in magnitude and direction by two adjacent sides OA and OD of a parallelogram OABD as shown in the figure.

Let θ be the angle between P and Q and R be the resultant vector. Then, according to the parallelogram law of vector addition, diagonal OB represents the resultant of P and Q

here R is the resultant of  two forces   p & q

(b) triangle law of forces:

it helps to find the resultant of two forces from the graph, closing side of the triangle gives resultant

(c) polygon law of forces:

 it is similar to the triangle law of forces  but applicable to more than 2 forces

(d) method of resolution :

 breaking force into a component like horizontal and vertical

in the given diagram assume F is given force then  Fx and Fy will be given by

fy = F sinФ 
fx = F cosФ 

(e) LAMI'S THEOREM :

 if there are three forces acting on a point, if  they are in equilibrium

now find vertical and horizontal component then find resultant

and direction is 

the sum of vertical forces/sum of horizontal forces

3 condition of equilibrium of forces :

 summation of horizontal force = 0

 summation of vertical force = 0

 summation of  moment = 0

4) MOMENT :  

moments gives only rotation without displacement

simply moment = force * perpendicular distance


area of triangle * 2= moment about the apex of   triangle ABC

5)VARIGNON'S THEOREM :

varignon's theorem said that,


algebraic sum of individual forces (f1,f2,f3,f4)about P point = moment of resultant force about P  point


f1*x  + f2*y + f3*z = R*l

here x,y,z, and l are the perpendicular distances

6)COUPLE: 

 forces which are equal in magnitude and opposite in direction called a couple

moment of couple =  only one force magnitude * distance between the force
                               = f*d
you have to know about F.B.D (free body diagram), and support reaction

7)BEAMS:  

(1)  simply supported beam
(2)  cantilever beam
(3)  overhanging beam
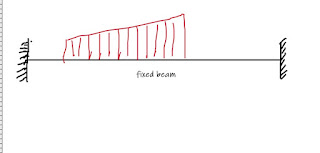
(4)  fixed beam
(5)  hinged beam
(6)  roller supported beam

figures are shown for better understanding

 

8)LOADINGS: 

(1)  concentrated load (point load):  in this diagram, P1 and P2 are the point load 

(2)  UDl (uniformly distributed load): notation of U.D.L is shown in the figure with red color

                          

(3)  UVL (uniformly varying load ):  notation of U.V.L is shown in the figure with red color

                                         

(4)  triangular load:   notation of triangular load is shown in the figure with red color

                                         

9)VALUE OF LOAD AND ACTION ON POINT:

here w is the load per unit length

   the value of UDL is  =W*span length =W*l             

   span length: where the load is distributed          
  and its action on the center of the span at   L/2

UVL:

value of UVL = ( (a*b)/2)*L

its act on L/3 from the apex side

in our example , apex is b

10)SUPPORT'S : 

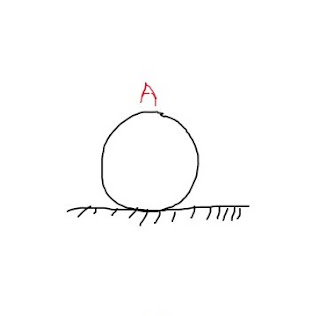
(1) HINGE SUPPORT:  hinge support  resist vertical and horizontal transformation but   allow rotation 

notation of hinge support given in diagram:

support reaction offered by a hinge support

(2) ROLLER SUPPORT:   free to rotate and transform along the surface where  the                                                   roller supported

notation of roller support given in diagram:

support reaction offered by a roller support

(2) FIXED SUPPORT: fixed support resist all translation and rotation

support reaction offered by a fixed support